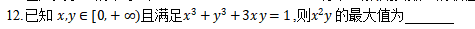
解:略
难点:条件中,等式的转化
中国文化背景
从中国古代数学发展的历程和数学本身的特征看,中国古代数学表现出对称性、统一性等科学美学特征。中国古代数学美的思想方法对数学、数学教育的发展曾经起到过积极作用,在今后的科学研究、数学教育中还会起到一定的启迪作用。尤其 《周易》的对称思想方法对中国传统思维具有重要意义,而且从某种意义上看,《周易》为现代数学多媒体教学的开展提供了思想渊源。另外《周易》又蕴涵着中学数学中集合、代数式、排列组合等中所含的对称思想方法。
《周易》的宇宙观一一对称
《周易》一书由两部分组成:一部分是64卦的卦辞和384爻的爻辞,称为《易经》;另一部分是解释卦辞与爻辞的注释和论述,称为《易传》。《周易》吸取了甲骨占卜中成对作双的基本概念,从复杂的自然现象和社会现象中抽象出阴、阳两个基本范畴。阴阳原义只是指日光的背向。向日为阳,背日为阴。后来周人将阴阳这一对范畴推广到世间万事万物,对我国的文化结构起着极其深远的影响,不论是中国哲学,还是中国科学,都是在这一基本的科学美学思想的指导下发展的。值得一提的是,《周易》认为凡是符合动态美原则的即为吉卦,体现了古代中国人民朴素的唯物主义哲学思想。
《周易》把阴阳的互相组合与作用,看成是世界万事万物生成变化的基础,而阴阳的平衡统一是自然和人类社会能够获得和谐发展的根本条件,只有这种和谐统一才能给世界带来稳定,否则就没有世界的稳定与发展。这是阴阳对称的重要意义。八卦的阴阳在总体上是对称平衡的。首先,八卦中阴爻和阳爻的总数是相等的,都是12个。其次,八卦在结构上也是两两相对,相反对称。再次,八卦在空间上的排列也是对称的。即东(震)、东南(巽)、南(离)、南西(坤)、西(兑)、北西(干)、北(坎)、北东(艮)八个方位,不断循环的一个结构。《周易》的这种对称思想,不仅对中国古代科学技术产生了深刻的影响,而且在现代科学研究中也有启发性作用。如张衡发明的地震测定仪中,八只青蛙所处的方位,与八卦在空间上的排列一致,既对称又循环,如图1;还有精湛的中国陶瓷艺术也折射出对称的光芒,如图2。《周易》与二进制具有相辅相成的关系:64卦中的每一卦都对应一个二进制的数。如果用1表示阳,用0表示阴,那么前四卦可分别表示为111111、000000、010001、 100010。《周易》八卦符号的选取与排列,一方面,非常讲究和谐与平衡,每一卦看上去都是一个


完美的对称图形;另一方面,将阴阳两字简化成 与——号,取两画为一卦,得四卦,再取三画为一卦,得八卦,正好与人们从自然界中抽象出来的八种事物一一对应。 然后由八卦再两两组合,便得64卦,再对每卦六个笔画分别作爻,则得384爻。卦和爻的演化,蕴涵一种数理之美,用现代数学理论来说,这就是中学数学中的排列组合问题。《周易•系辞》说:“方以类聚,物以群分。”这里所说的“类”与“群” 就与数学中的“集合”概念非常相近。而集合论是现代数学的基础,它不仅渗透到数学的各个领域,也渗透到许多自然科学和社会科学领域。将八卦用集合论的语言描述, 就会更方便、更清楚、更精确。
八卦与代数式也有一定的联系:令表示阴爻,
表示阳爻,并规定
,则当
时,我们所熟悉的平方和公式就成为
,对应于八卦的四象,当
时,立方和公式就成了
,正好对应于四象所生的八卦。八卦在矩阵、群论、概率论中都有其数学解释,我们接下来也会挑选解释。
教材出处
新人教A版

课标变化
新课标要求通过梳理等式的性质,理解不等式的概念,掌握不等式的性质。
而旧课标要求通过实例感受在现实世界和日常生活中存在着大量的不等关系,没有关于等式性质的要求。
低维了解(水平一)
三次多项式因式分解
首先初中时学了立方和公式,
所以,那么可以推导出下面这个关系式
令即可得
中维迁移(水平二)
此题和教材中一题有什么联系?和很多大考甚至是高考真题有什么联系?
读者思考后直接给出答案
【定义1】一个元代数式
,如果交换任意两个字母的位置后,代数式不变,即对于任意的
(
),都有
那么,就称这个代数式为元对称式,简称对称式。
例如,都是对称式。
如果元对称式是一个多项式,那么称这个代数式为
元对称多项式。
由定义1知,在对称式中,必包含任意交换两个字母所得的一切项,例如,在对称多项式中,若有
项,则必有
项;若有
项,则必有
,
项,这些项叫做对称式的同形项,同形项的系数都相同。
根据对称多项式的定义,可以写出含个字母的对称多项式的一般形式,例如,含有三个字母
的二次对称多项式的般形式是:
【定义2】如果一个元多项式的各项的次数均等于同一个常数
,那么称这个多项式为
元
次齐次多项式。
由定义2知,元多项式
是
次齐次多项式,当且仅当对任意实数
有
。
例如,含三个字母的三元三次齐对称式为:
。
【定义3】一个元代数式
,如果交换任意两个字母的位置后,代数式均改变符号,即对于任意的
,都有
那么就称这个代数式为元交代式。
例如,均是交代式。
【定义4】如果一个交代数式
,如果将字母
以
代
,
代
代
代
后代数式不变,即
那么称这个代数式为元轮换对称式,简称轮换式。
显然,对称式一定是轮换式,但轮换式不一定是对称式。例如,是对称式也是轮换式;
是轮换式,但不是对称式。
对称式、交代式、轮换式之间有如下性质(基础,重要,证明略):
(1)两个同字母的对称式的和、差、积、商仍是对称式;
(2)两个同字母的交代式的和、差是交代式它们的各、商是对称式;
(3)同字母的对称式与交代式的积、商是交代式;
(4)两个同字母的轮换式的和、差、积、商是交代式;
(5)多变无的交代多项式中必有其中任意两变元之差的因式。
PS:例如,二元基本对称多项式是指,
三元基本对称式是指
从更高的维度(高等数学)来看,任何一个元对称多项式都可以表示为基本对称多项式的多项式。这个结论对解题的指导作用。
同时直接给出解题的一些常用技巧和疑问供读者思考,一定要思考,因为这儿想不明白会落入命题者陷阱。
(1)若是对称式,则在解题中可设
。(为什么?)
(2)若是对称式,则当
满足性质
时,
也满足性质
。
(3)若是轮换式,则在解题中可设
最大(小),但不能设
。(为什么?)
(4)若是轮换式,且
满足性质
,则
也满足性质
。
(5)若是交代多项式,则
是
的因式,即其中
是对称式。
,其中
是对称式。
在利用对称式作因式分解时,齐次对称多项式,齐次轮换对称多项式,齐次交代多项式是常用的。
齐次对称多项式的一般形式:
(1)二元齐次对称多项式
一次:,
二次:
三次:
(2)三元齐次对称多项式
一次:
二次:
三次:
判定是否为多项式
的因式的方法是:令
,计算
,如果
,那么
就是
的因式,在实际操作时,可首先考虑
的如下特殊情形:
举例1分解因式。
解 显然是三次齐次对称多项式。
令,即
代入得
,
所以是
的一个因式,故它的另一个因式必为二次齐次对称式,所以
可表示为
令得
令得
所以(观察低维区别)
举例2分解因式。
解 显然是关于
的四次齐次多项式,显然无
的因式
故可设
令不同取值可得
于是
根据课程标准,由等式迁移至不等式
- 不等式对称和轮换对称式的定义
在一个不等式中,若把其中任何两个字母对调位置后,这个不等式不变(如①
,其中
), 我们便称此不等式是关于
对称的。如果把不等式中的字母
按一定顺序依次轮换(如
换成
,
换成
,...,
换成
)后不等式不变(如②
),我们便称此类不等式是关于
轮换对称的。
- 对称式与轮换对称不等式的性质
由定义易知,对称的不等式一定是轮换对称的(如①),而轮换对称的不等式却不一定是对称的(如②就不是对称的)。
关于对称的不等式,由于
互换后原不等式不变,因此要想怎么排列他们的大小顺序,只要调换其位即可,故我们可任意排列
的大小顺序(如在①中可设
),而关于
是轮换对称的不等式则不能任意排列其字母的大小顺序,而只能做较弱的排列,如
,
,...,
,即某一个是其中的最大或最小(如②中可设
,
),因为我们总可以通过轮换把某个字母调整到最小或最大的位置。
- 取得最值的判定
轮换对称式取到最值时往往各地位轮换对称的变量取值相等。在这种情况下我们可以简化问题为先判断最值和取到最值的条件,在转化为不等式证明问题(此时取等的条件也作为一个解决不等式证明的重要提示)。
当然,并不是所有轮换对称式取最值的条件都是上述,所以我们尽可能用特值等方法验证来舍弃显然不合理的假定,确认判断正确后再转化为证明问题,这样可以减少无用功。值得注意的是,判断各变量相等时取到的是最大还是最小值与题目要求比对是十分必要的。
- 轮换对称式常见的处理方法
- 凑项法(最常用)
在判断出最值后,利用基本不等式等号成立的条件凑项证明,只要领悟添项的技巧,完全可以程式化证明一类不等式。主要细分为凑项降幂法、凑项升幂法、凑项去分母法、凑项平衡系数法。
基本思路:判断该题为轮换对称式;通过条件得出取最值时各字母或参数的值;判断是最大或最小值,抓住其中一项深入研究,构造均值不等式的其他项,再运用均值不等式加以证明。
上述各种凑项方法不是相对独立的,可以交替使用,但凑项的关键是在求和时能利用已知条件,并能取到等号。
- 求配偶式法(即(1)的进化版本)
当直接配凑较为困难时我们可以通过先设待定系数求解的方法找到要凑得项。充分利用轮换对称式等式的结构特点以及等号成立的条件为导向,运用待定系数法构造配偶式,然后运用均值不等式等号成立的条件以及所证轮换对称不等式等号成立的条件求出待定系数,从而使所证不等式获得证明。其中设配偶式求配偶因子是该方法的关键一步和核心部分,也是它与方法(1)的主要区别。
- “非常规最值”的应对方法
前几个方法中,首要是确认在各变量取值相等时取到最值,这类最值问题称为“常规最值”。然而并非所有的轮换对称式都满足这一要求,因而面对一些“非常规最值”问题,也有一些特定的其他方法,如:构造不等式法、导数法和图像法等。
高维创新(高三综合水平三)(竞赛与强基计划)
1、与矩阵和函数压轴题,太多太多了,懒得打字了,只给出这一题的证明及几个性质推论完事
把所有行加到第一行再提取公因子得
性质n:(特征值,范特蒙德矩阵可证)
可得推论:
One当时
Two
Three
Four,其中
…………………………………………
2、与圆锥曲线:高二练习题:是什么曲线(直线与双曲线)
统称为圆锥曲线,一大堆迁移和创新不打了
|
判别式 |
一般情形 |
特殊情形 |
|
|
椭圆 |
一点或无图形一点 |
|
|
双曲线 |
两相交直线 |
|
|
抛物线 |
两平行直线或一直线 |
通过坐标轴的平移和旋转,可以把一般方程变为标准的圆锥曲线方程(极坐标或三角换元与参数方程)