此题命制背景

1. 切线的性质（超纲）
2. 两条直线关于第三条直线对称的斜率关系（来自教材中课后习题的改编）

所以第二问为竞赛题，超纲，第三问不超纲，但都可以了解，多学点总没错，切线和切点实际上是特殊的极点极线，这个暂时就先不讲了，先来看看在本题中用到的切线性质如下：

从一个焦点发出的光线，经过椭圆壁的反射，所有反射光
一定聚焦于另一焦点。因此过椭圆上任何一点作切线，那么该切线的法线一定平分切点与两焦点的连线的夹角(入射角=反射角)。

即椭圆的两个焦点分别与切点相连,这两条连线与切线夹角相等

证明如下（偏微分，超纲，了解即可，也可用高中知识证明，但比较麻烦）：

令椭圆为 x²/a² + y²/b² = 1, 在上面取点P(acosθ, bsinθ)
对椭圆求导, 2x/a² + 2yy'/b²= 0, y' = -b²x/(a²y)
过P点的切线斜率k = -b²acosθ/(a²bsinθ) = -bcosθ/(asinθ)
过P点的切线的垂线(法线)斜率k' = -1/k = asinθ/(bsinθ)
法线为: y - bsinθ = [asinθ/(bsinθ)](x - acosθ)
令y = 0, x = -b²sinθcosθ/(asinθ) + acosθ = (a² - b²)(cosθ)/a = c²(cosθ)/a
法线与x轴的焦点为Q(c²(cosθ)/a, 0)
F1(-c, 0), F2(c, 0)
PF1的方程为: (y - 0)/(bsinθ - 0) = (x - c)/(acosθ - c)
整理得(bsinθ)x - (acosθ + c)y + bcsinθ = 0 （i）
Q与其距离为d1 = |(bsinθ)*c²(cosθ)/a - 0 + bcsinθ|/√[(bsinθ)² + (acosθ + c)²]
分母中根号下的部分 = b²sin²θ + a²cos²θ + 2accosθ + c² = b²sin²θ + (b² + c²)cos²θ + 2accosθ + c²
= b²(sin²θ + cos²θ) + c²cos²θ + 2accosθ + c²
= b² + c² + 2accosθ + c²cos²θ = a² + 2accosθ + c²cos²θ = (a + ccosθ)²
分子= |(bcsinθ)(ccosθ + a)|/a
d1 = |(bcsinθ)(ccosθ + a)|/[a(a + ccosθ)] = (bc/a)|sinθ|
将(i)中的c变号得PF2的方程, 类似地可得d2 = (bc/a)|sinθ|
即Q与PF1和PF2等距离, PQ为∠F1PF2的平分线；直角减去相等的角结果相等，即PF1, PF2与切线夹角相等

图像如下：

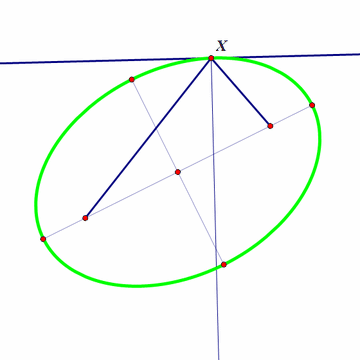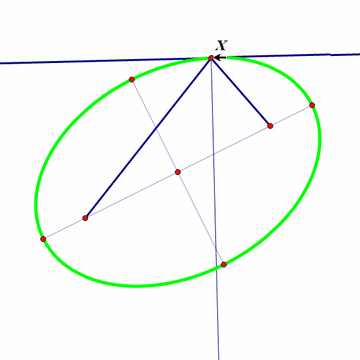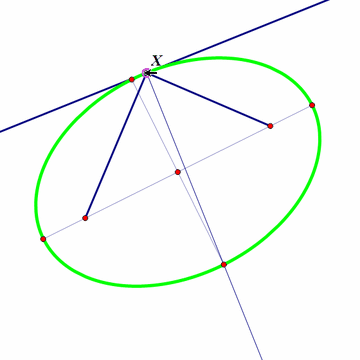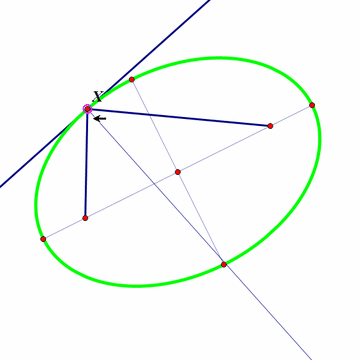
显然切点与两个焦点的连线与切线和法线都对称

设直线的斜率为k，两条对称直线的斜率为a、b，则有这样的关系：

|(k-a)/(1+ka)|=|(b-k)/(1+kb)|

自行证明

有个类似的之前江苏的小题也是可以用对称快速解决的，如下：

已知圆O：x²+y²=4，若不过原点O的直线l与圆O交于P、Q两点，且满足直线OP、PQ、OQ的斜率依次成等比数列，则直线l的斜率为___．