何谓数学?随即向人们提问,你可能获得的答案是,“是有关数字的一种学问”。如果继续追问他们所谓的学问是哪一种,你或许可以诱导他们提出譬如“那是一种有关数字的科学”之描述。不过,这大概是你可以得到的最多的信息。而这一种有关数学的描述,在大约2500年前,就已经不再正确了。
在这样一个巨大的误导之下,你所随机抽样的人们无法体会数学研究是一种兴旺且无所不在的活动,或是接受数学经常相当程度地贯穿我们日常生活与社会大部分活动的看法。这毫不令人意外。
事实上,“何谓数学”这个问题的答案,在人类历史过程中,已经数度更易了。
到公元前500年左右,数学的确是有关数字的一中学问。这是古埃及和古巴比伦时期的数学。在这些文明中,数学所包括的,几乎都以算术为主。他大部分属功利取向,而且充满了“食谱”的特色(比如,“对一个数字这样做,再那样做,你将会得到答案”)。
从大约公元前500年到公元300年的这一时期(中考最重要的800年),是希腊数学的时代。古希腊的数学家主要关心几何学。诚然,他们按几何方式,将数字视为线段长之度量,而当他们发现有数字缺乏对应的线段长时,有关数字的研究就停顿下来了。对于希腊人而言,由于他们强调几何学,所以,数学不止研究数字,而且也是有关形状的学问。
事实上,幸亏有希腊人现身,数学才进入研究领域,而不只是度量、计算和会计等技巧的大杂烩。希腊人对于数学不止存功利取向,他们视数学为一种知性探索,其中包含了美学与宗教成分(美育在数学中的情感态度与价值观可以充分体现,但是如果没有真正接触过艺术,备课的难度会很大)。泰勒斯引进了如下想法:数学上精确陈述的断言(断言这个词我现在看到都头皮发麻,这些人数学的感觉好到有毒),都可以被一个形式的论证逻辑的证明出来。这一创新标志着“定理”——数学的基石——的诞生(也正是因为这个基石,古代国外的数学传承做的比国内好,这个基石背后的逻辑在我们的教学中也有挑战)。
对希腊人而言,这一进程在欧几里得《几何原本》出版时攀上了巅峰。这一部西方数学经典,在历史上因流传度仅次于《圣经》而闻名。看这本书不光要看内容,更重要的是要看作者是如何建立一个几乎不可摧毁的大厦的,如何让这座大厦对后代的传承起到决定性作用的。
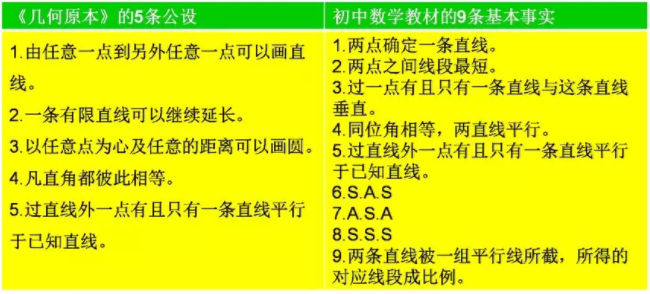
附:《几何原本》与初中数学教材中的公理体系
《几何原本》与初中数学教材中的公理体系
李文革
欧几里得的《几何原本》大约成书于公元前三世纪左右,它是用公理建立起演绎体系的最早典范。两千多年来,它一直是人们学习演绎推理的权威教材。为了使平面几何内容使教师易教和学生易学,遵循学生的认知规律,初中数学教材对《几何原本》中的公理体系进行了教学处理,给出了一个弱化的公理体系,让学生感受公理化思想。《几何原本》中的公理体系与初中数学教材中的公理体系是不完全相同的。
一、《几何原本》中的公理体系
《几何原本》分为13卷,共465个命题,涉及平面几何、立体几何及数论等领域。第1卷给出了23条定义、5条公设和5条公理,这些定义、公设和公理就是《几何原本》中的公理体系证明的出发点。

5条公设:
(1)由任意一点到另外任意一点可以画直线。
(2)一条有限直线可以继续延长。
(3)以任意点为心及任意的距离可以画圆。
(4)凡直角都彼此相等。
(5)同平面内一条直线和另外两条直线相交,若在某一侧的两个内角的和小于二直角的和,则这二直线经无限延长后在这一侧相交。(与平行公理等价)
显然第5公设与其他公设不同,它的行文较长,远不是那种不证自明的真理。有证据表明,欧几里得本人在《几何原本》第1卷的演绎证明中一直尽力避免应用这一平行公设,在前28个命题的证明过程中,他对其他公设都运用自如,而唯独一直没有使用第5公设。
5条公理:
(1)等于同量的量彼此相等。
(2)等量加等量,其和仍相等。
(3)等量减等量,其差仍相等。
(4)彼此能重合的物体是全等的。
(5)整体大于部分。
公设是针对几何的,公理更具一般性,不仅仅针对几何。长期以来,人们认为公理4具有几何特征,应归入公设的范围。
二、初中数学教材中的公理体系
《义务教育数学课程标准(2011年版)》列出了9条基本事实作为初中数学教材中的公理体系证明的出发点(如下表)。之所以称“基本事实”,而不称公理,其原因在于9条基本事实中大部分都是《几何原本》中的公理体系的定理;而且这9条基本事实也不具有公理体系所应具有的独立性、相容性和完备性。《几何原本》中的公理体系与初中数学教材中的公理体系证明的出发点如下表所示。
如S.S.S,初中数学教材把它作为基本事实,而《几何原本》把它作为定理。为了证明该定理,欧几里得采用了下列方法。
要证明三边对应相等的△ABC和△A′B′C′全等,只需证明两个三角形能完全重合,即只需把某一对应边,例如BC和B′C′重叠,证明A与A′重合即可。如图1所示,A与A′的情况只有下列4种情况:
(1)A和A′不包含在另一三角形中。
(2)A和A′之一在另一三角形内部。
(3)A和A′之一在另一三角形边上。
(4)A和A′重合。

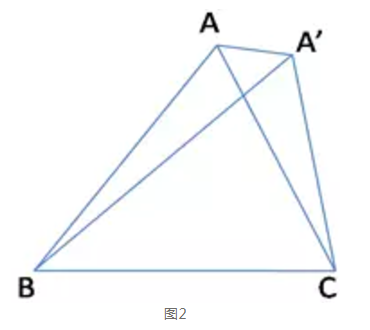
- 对于情况1,如图2,连结A 和A′。
因为△ABA′是等腰三角形,
所以底角相等,即∠BAA′=∠BA′A。
由图2可知∠CAA′<∠BAA′=∠BA′A<∠CA′A,即
∠CAA′<∠CA′A。
由于CA=CA′,
所以∠CAA′=∠CA′A。
于是矛盾,因此情况1不成立。
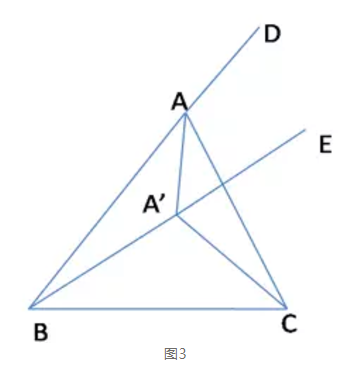
- 对于情况2,如图3,分别延长BA、BA′至D、E。
因为BA=BA′,
所以∠BAA′=∠BA′A,
所以∠DAA′=∠EA′A。
由图3可知∠CAA′<∠DAA′=∠EA′A<∠CA′A,即
∠CAA′<∠CA′A。
由于CA=CA′,
所以∠CAA′=∠CA′A。
于是矛盾,因此情况2不成立。
- 对于情况3,显然不成立。
综上,只有情况4成立,即A和A′重合。
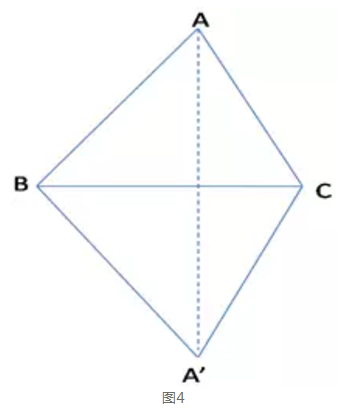
在欧几里得之后约500年(3世纪),一个叫费洛的几何学家通过把两个三角形如图4放置,连结AA′,利用“等边对等角”得出∠BAC=∠BA′C,再利用S.A.S(S.A.S是第1卷的第4个命题,S.S.S是第1卷的第8个命题)证明△ABC≌△A′B′C′。
三、《几何原本》与初中数学教材中的
公理体系证明举例
初中数学教材作为基本事实的三角形全等的三条判定定理S.A.S、A.S.A、S.S.S,在《几何原本》中都是定理,其中,S.A.S是第1卷的第4个命题,S.S.S是第1卷的第8个命题,A.S.A是第1卷的第26个命题。
在上述欧几里得证明S.S.S的方法中,他用到“等边对等角”这一等腰三角形的性质。在《几何原本》中,“等边对等角”是第1卷的第5个命题,排在作为第1卷第8个命题的S.S.S的前面,因此,欧几里得用“等边对等角”证明S.S.S是无可厚非的。这与初中数学教材的安排刚好相反,初中数学教材是在给出三角形全等的三条判定定理S.A.S、A.S.A、S.S.S后,用三角形全等的判定证明“等边对等角”的(参见华东师大版初中数学教材八年级上册第79页)。

由于在《几何原本》中S.A.S是第1卷的第4个命题,而“等边对等角”是第1卷的第5个命题,因此欧几里得运用S.A.S对“等边对等角”给出的证明如下:
已知:如图5,在△ABC中,AB=AC。
求证:∠B=∠C。
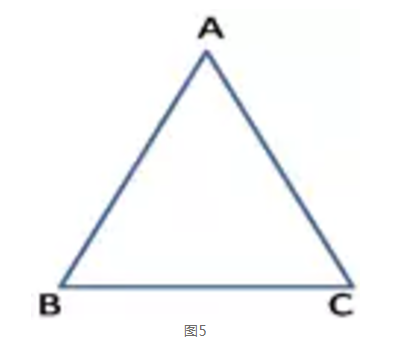
图5
证明思路:如图6,在BD任取一点F,在AE上截取AG=AF,连结FC、GB。先运用A.S.A证明△AFC≌△AGB,得出∠ABG=∠ACF;再运用A.S.A证明△BCG≌△CBF,得出∠CBG=∠BCF。最后根据“等量减等量其差相等”得出∠ABC=∠ACB。
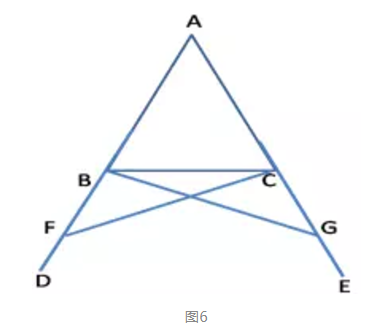
图6
在欧几里得之后约500年(3世纪),一个叫巴伯斯的人仅仅利用图5,通过运用S.A.S证明△ABC≌△ACB,非常简洁地得出了∠B=∠C。
由于欧几里得的证明复杂、难懂,这一定理以“笨人过不去的桥”著称。之所以有此说法,一是因为欧几里得的图形有点像座桥;二是因为许多对几何知识了解不深的学生都难于理解这一定理的证明,也就是无法跨过这座桥,进入《几何原本》的其他部分的学习。
通过《几何原本》和初中数学教材对这一定理的不同证明,我们感受到:如果初中数学教材严格按照《几何原本》的公理体系呈现,对初中学生的学习显然会带来很大困难。因此,《义务教育数学课程标准(2011年版)》对平面几何内容的处理是适当的,既遵循了数学的发展规律,又遵循了教育和初中生认知发展的规律。